Transformation¶
The interface often needs to handle 3D poses or transformations between two coordinate systems. These transformations have six degrees of freedom and are always represented by the same structure of nodes, described below.
Formats
Object/Transformation- This is the node of the parameter or return value, representing a transformation of pose in 3D space. Its sub nodes contain the transformation parameters.
Rotation (Object)- Sub node containing the 3D rotation part of the transformation specified via angle and rotation axis. Its sub nodes contain the transformation parameters.
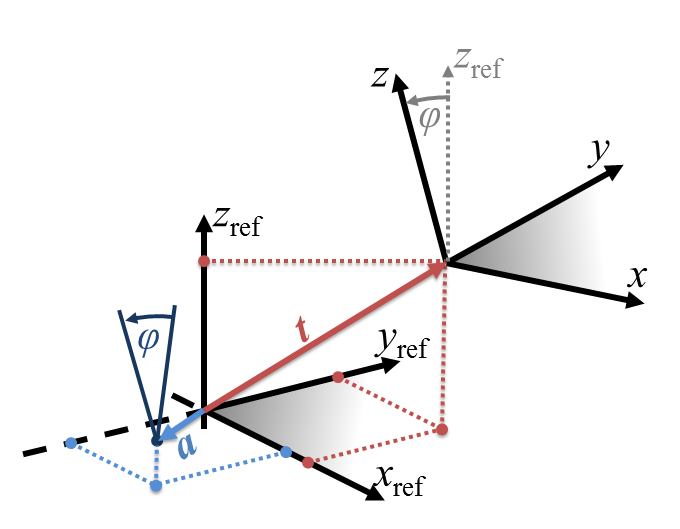
Angle - The rotation angle \(\varphi\) in radians
Axis - A Vector specifying the axis of rotation, This vector is normalized when rotations are returned via the interface. Although it does not need to be normalized when specifying a rotation.
0 (Number) - The x component of the rotation axis vector.
1 (Number) - The y component of the rotation axis vector.
2 (Number) - The z component of the rotation axis vector.
Translation (Array/Vector)- A Vector specifying the translation part \(t\) of the transformation interface. Although it does not need to be normalized when specifying a rotation.
0 (Number) - The x component of the rotation axis vector.
1 (Number) - The y component of the rotation axis vector.
2 (Number) - The z component of the rotation axis vector.
Inverse (Boolean, optional)- When set to true, the transformation will be inverted before it’s used.
Note
Any rotation in 3D space can be represented as a rotation around a single axis.
Shorthand Formats
When specifying transformations or poses with zero translation or rotation, it is allowed to set the Rotation or Translation nodes to the Number value 0, or to completely omit the corresponding node. Transformations stored in the tree or output from commands will always have the full format.
Interpretation
Poses and transformations within NxLib are always specified as the relative pose of the target system inside the reference system. When the transformation is represented as a 4x4 homogeneous transformation matrix the columns of the upper left 3x3 matrix would represent the axis directions \(( x, y , z )\) of the target system inside the reference system, and the upper right 3x1 column vector indicates the location of the target origin inside the reference system (\(t\)). Note however that in NxLib’s transformation nodes the rotation part is represented as an 3x1 axis vector \(a\) and a rotation angle \(\varphi\). If you need to convert between different formats or invert transformations you can use the ConvertTransformation command.
There are two equivalent ways on how to interpret the transformations and poses:
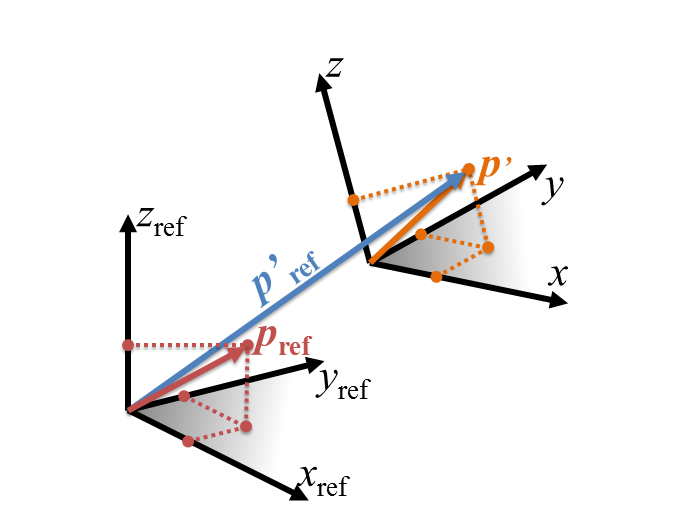
Active Transformation: Transformations and poses can be interpreted as active transformations in their reference system: Applying the transformation to a point \(p_{ref}\) in the reference system will move the point to the corresponding location of the target system and result in the coordinates \(p_{ref}^{'}\) in the reference system.
Passive Transformation / Change of Basis: Another interpretation of the transformation is a change of basis from the target pose to the reference system. Applying the transformation to a point \(p^{'}\) in the target system will yield the coordinates \(p_{ref}^{'}\) in the reference system.
Note
The two formulations are mathematically equivalent and both define the same transformation direction.